Calculadora regla de tres simple directa
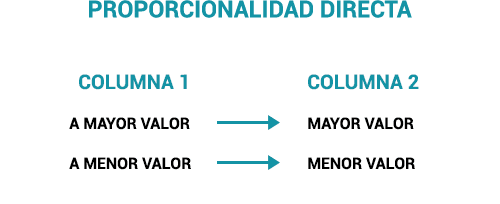
Utilízala para resolver problemas de regla de tres simples con valores que son directamente proporcionales. Es decir cuando los valores de la columna 1 aumentan o disminuyen, los valores de la columna 2 aumentan o disminuyen de igual manera.
Ejemplo regla de tres simple directa:
2 litros de pintura alcanzan para pintar una pared de 36 m². ¿Cuántos m² se podrían pintar con 7 litros?
Entre más litros de pintura se usen, más m² se pueden pintar. Así mismo entre menos litros se usen, alcanzara para una menor área.
Relación de proporcionalidad directa:
Más litros = Mayor área pintada
Menos litros = Menor área pintada
Calculadora regla de tres simple inversa
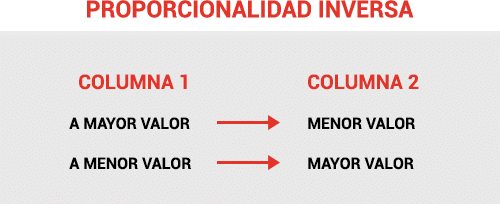
Utilízala para calcular problemas de regla de 3 simples en donde las magnitudes de la columna 1 son inversamente proporcionales a las de la columna 2. En otras palabras en la regla de tres inversa, cuando los valores de la columna 1 aumentan o disminuyen , los valores de la columna 2 disminuyen o aumentan de manera opuesta.
Ejemplo regla de tres simple inversa:
3 obreros construyen un muro en 5 horas. ¿Cuántas horas se tardarían 7 obreros?
Entre más obreros trabajen, menos horas demorarán. Así mismo, entre menos obreros trabajen, más horas tardarán.
Relación de proporcionalidad inversa:
Más obreros = Menos tiempo
Menos obreros = Más tiempo
Calculadora regla de tres compuesta directa
Con la calculadora de regla de 3 compuesta directa podrás resolver problemas de proporcionalidad múltiple directa, donde están involucradas tres magnitudes. Si una magnitud aumenta o disminuye, la magnitud de la incógnita aumenta o disminuye de igual manera.
Ejemplo regla de tres compuesta directa:
Si 7 botellones de aceite de 3 litros cada uno pesan 7 kilos. ¿Cuánto pesan 3 botellones de 6 litros cada uno?
Si aumentamos la cantidad de botellones de aceite, el peso también aumentará. Por otro lado, si aumentamos la cantidad de galones, el peso aumentará en igual proporción.
Relación de proporcionalidad directa.
Más botellones = Más kilos
Más galones = Más kilos
Calculadora regla de tres compuesta inversa
Utiliza la calculadora de regla de 3 compuesta inversa para resolver problemas de proporcionalidad múltiple inversa, donde cuentas con 3 magnitudes. Cuando los valores son inversamente proporcionales, el aumento o disminución de alguna magnitud, impactará inversamente a los valores de la magnitud donde se encuentra la incógnita.
Ejemplo regla de tres compuesta inversa:
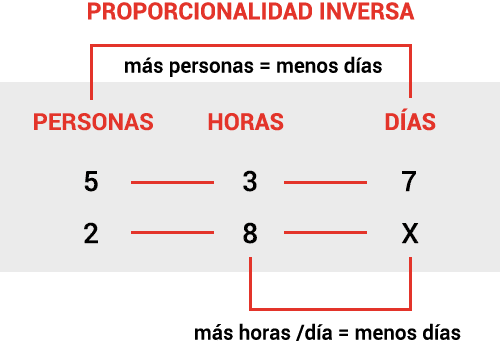
5 personas tardan 7 días digitalizando un libro trabajando 3 horas diarias. ¿Cuanto tardan 2 personas trabajando 8 horas diarias)
Si el número de personas trabajando aumenta, el libro quedará digitalizado en menos días. De igual forma, si el número de horas diarias aumenta, el número de días de edición también disminuye.
Relación de proporcionalidad inversa:
Más personas trabajando = Menos días
Más horas diarias de trabajo = Menos días
Aprende más sobre el uso de excel aquí → Excelalinstante.
Calculadora regla de tres en excel
Para aquellos que prefieren utilizar excel para todos sus cálculos, hemos creado un sencillo tutorial de 3 pasos donde aprenderás cómo calcular una regla de 3 en excel.
También podrás descargar nuestra plantilla con la fórmula configurada, donde podrás aplicar la regla de tres directa e inversa en excel, para que la tengas a la mano y la utilices en cualquier momento, sin necesidad de sacar tu calculadora o tener conexión a internet.

Para qué puedes utilizar la calculadora de regla de tres online
Existen múltiples escenarios en los que puedes aprovechar nuestra calculadora de regla de 3 online. Aquí mencionamos algunas aplicaciones útiles de la regla de tres en contexto para resolución de problemas de la vida cotidiana.
- Calcular porcentajes
- Cálculo de dosis de medicamentos
- Cálculo el salario base
- Calcular comisiones
- Cálculo de intereses
- Calcular tiempo por tarea
- Calcular inversiones
- Calcular escalas
- Calcular metros por minutos
- Calcular notas o calificaciones
- Calcular velocidad
- Calcular distancias
- Calcular vacaciones
- Calcular liquidacioens
Para conocer más términos sobre finanzas y economía, puedes entrar a: Finanzas.Wiki