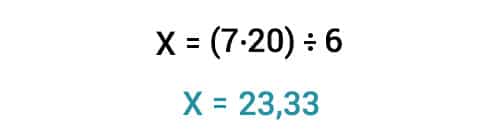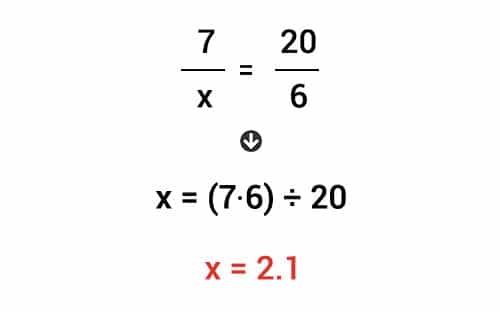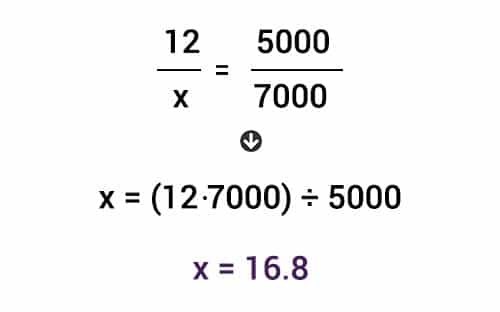Cuando hablamos de que es una regla de tres compuesta, nos referimos al igual que en la simple, a problemas donde se relacionan magnitudes proporcionales. Pero este caso, la regla de 3 compuesta se diferencia porque en esta operación matemática trabajamos con tres o más magnitudes. En este artículo aprenderás cómo se utiliza en sus tres tipos de proporcionalidad (directa, inversa y mixta) y ejemplos claros de su solución.
Cómo resolver una regla de tres compuesta
Existen tres tipos de regla de tres compuesta y son utilizados para resolver tres tipos de casos de proporcionalidad diferentes. Estas son la directa, inversa y mixta. A continuación encontrarás una explicación fácil de en qué consisten, cuando usarlos y algunos ejemplos resueltos.
Regla de tres compuesta directa
Cuando la equivalencia es directa, es decir, cuando una magnitud aumenta o disminuye, y cómo resultado la otra aumenta o disminuye en igual proporción, estamos hablando de regla de tres compuesta directa.
Ejemplo regla de tres compuesta directa:
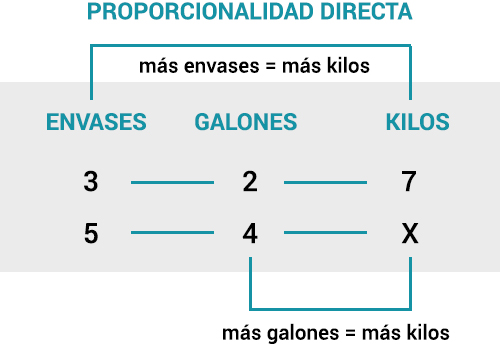
Si 3 envases de pintura de 2 galones cada uno pesan 7 kilos, ¿Cuánto pesan 5 envases de 4 galones cada uno?
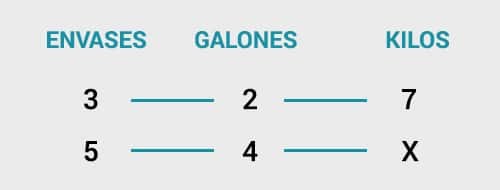
Al comparar la relación de las magnitudes que conocemos con el valor desconocido X, podemos cómo este es un claro ejemplo de regla de tres compuesta directa, ya que las magnitudes son directamente proporcionales.
más envases = más kilos
más galones = más kilos.
Para resolver este problema con mayor facilidad, escribimos las relaciones en fracciones para despejar la incógnita. La primera fracción es donde se encuentra la incógnita, luego igualamos y multiplicamos entre sí las otras dos fracciones:Finalmente, despejamos el valor x haciendo productos cruzados con el resultado obtenido de la multiplicación de los fraccionarios del lado derecho.
Respuesta: 5 envases de 4 galones cada uno pesan 23.33 Kilos
Regla de tres compuesta inversa
La regla de 3 compuesta inversa es utilizada para resolver operaciones proporcionalidad inversa con 3 o más magnitudes . Cuando los valores son inversamente proporcionales, el aumento o disminución de un valor afectara inversamente a los valores de la columna donde se encuentra la incógnita.
Ejemplo regla de tres compuesta inversa:
5 obreros tardan 11 días en reparar el piso de una casa, trabajando 6 horas diarias. ¿Cuántos días tardarán 7 obreros trabajando 8 horas diarias?
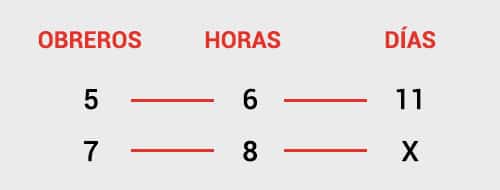
Si comparamos la cantidad de obreros con la cantidad de días que estos toman en hacer el trabajo, vemos que entre más obreros, el trabajo tomará menos días. Así mismo, si comparamos la cantidad de horas diarias de trabajo con la cantidad de días, podemos ver que entre más horas, el trabajo tomará menos días. Esto es un claro ejemplo de regla de 3 compuesta con proporcionalidad inversa.
más obreros = menos días
más horas al día = menos días
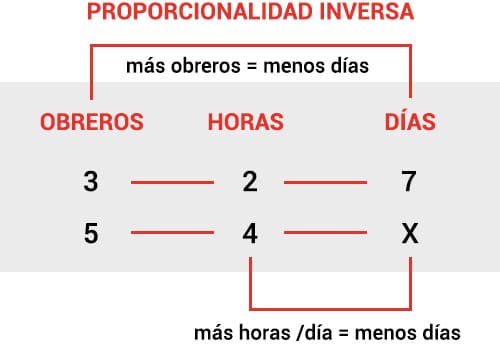
Para resolver este ejercicio con mayor facilidad, primero escribimos las relaciones en fracciones y pasamos la columna donde se encuentra la incógnita a la primera posición con el fin de de despejar la X.
A diferencia de la regla de tres compuesta directa, en esta ocasión debemos invertir los fraccionarios de las magnitudes que conocemos, dado a que que las relaciones son inversamente proporcionales.
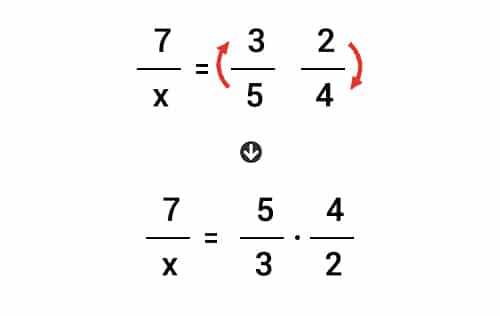
Finalmente para hallar la respuesta, multiplicamos los fraccionarios de la derecha entre sí, y con el resultado obtenido hacemos productos cruzados para despejar la x.
Respuesta: 7 obreros trabajando 8 horas diarias tardarían 2.1 días reparando el piso de la casa.
Regla de tres compuesta mixta
Esta regla de tres es utilizada cuando tenemos un problema donde entre las magnitudes encontramos relaciones de proporcionalidad directa y también inversa.
Ejemplo regla de tres compuesta mixta:
Una constructora contrata a 4 obreros para pintar una casa de 1000 m2 en 12 horas. ¿Cuánto tardarían en pintar una casa de 1.750 m2 si contrataran a 5 obreros?
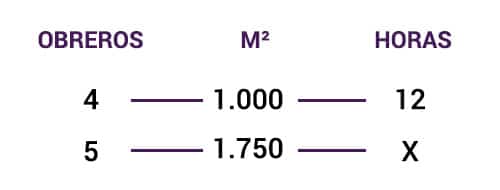
Al comparar la relación de las dos magnitudes que conocemos (obreros y metros cuadrados) con los valores de columna donde se encuentra el valor que desconocemos (horas), podemos ver como una relación es de proporcionalidad directa y la otra de inversa.
más obreros = menos horas
más metros cuadrados = más horas
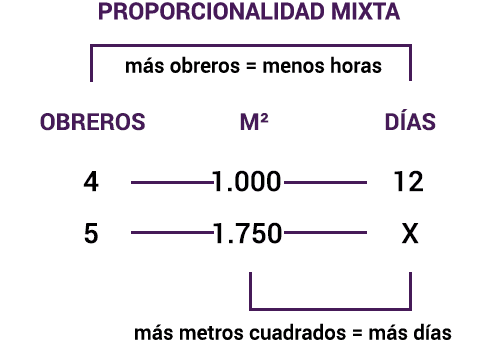
Al igual que en la regla de tres compuesta directa e inversa, lo primero que debemos hacer es escribir las relaciones en fracciones y pasar la columna donde se encuentra la incógnita a la primera posición para así poder despejar la x.
En este caso, para la relación de proporcionalidad inversa debemos invertir los fraccionarios mientras que la relación de proporcionalidad directa se queda en su posición original. En el ejemplo vemos que entre más obreros trabajen, va a tomar menos tiempo terminar el proyecto. Esto nos indica que la magnitud de número de obreros tiene proporcionalidad inversa.
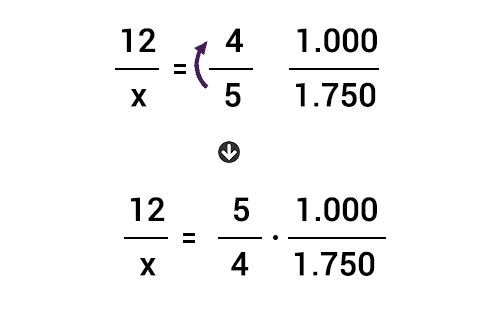
Finalmente para hallar la respuesta, multiplicamos los fraccionarios de la derecha entre sí, y con el resultado obtenido hacemos productos cruzados para despejar la x.
Respuesta: 5 obreros tardarían 16.8 horas pintando una casa de 1.750 m2
Calculadora online regla de tres compuesta
Con nuestra calculadora online de regla de tres compuesta podrás resolver fácilmente ejercicios de proporcionalidad directa e inversa de tres magnitudes.
Calculadora online regla de tres simple directa e inversa
Con nuestra calculadora online de regla de tres simple podrás resolver fácilmente ejercicios de proporcionalidad directa e inversa de dos magnitudes.